Queraberrationen der reinen Abbildungsfehler
Um die optische Abbildungsqualität eines Fernglases bewerten oder vergleichen zu können, bedient man sich bevorzugt der Darstellung der Queraberration für verschiedene Feldpunkte. Die Interpretation dieser Darstellungen erfordert jedoch einige Kenntnisse und Erfahrung. In der Praxis ergibt sich immer eine Überlagerung aus verschiedenen Fehleranteilen. Deshalb sollen hier einige ausgewählte wichtige Abbildungsfehler isoliert voneinander dargestellt werden, um charakterisitische Merkmale besser verdeutlichen zu können.
Die Abweichungen der Strahlen vom paraxialen Bildpunkt lassen sich theoretisch mit einem Term beschreiben, der aus 5 Summanden besteht. Entsprechend diesen 5 Summanden klassifiziert man die auftretenden Abbildungsfehler in die 5 monochromatischen Aberrationen 3. Ordnung. Die 5 unten gezeigten Terme sind proportional zu der Querabweichung vom paraxialen Bildpunkt dy senkrecht zur optischen Achse, wobei h der Abstand des Objektpunktes von der optischen Achse und q und j die Position des Strahlendurchstoßpunktes auf der Linse in Polarkoordinaten mit dem Durchstoßpunkt der optischen Achse als Nullpunkt sind:
dy
|
~ |
r 3cosq hr 2(2+2cos2q ) h2r cosq h2r cosq h3 |
sphärische Aberration Koma Astigmatismus Bildfeldwölbung Verzeichnung |
Von diesen Seidelschen Bildfehlern sollen hier betrachtet werden:
Über diese Bildfehler 3. Ordnung hinaus gibt es weitere Bildfehler höherer Ordnung, die hier aber nicht weiter dargestellt werden. Der Verzeichnung selbst ist ein eigenes Kapitel gewidmet, da sie sich in der Darstellung der Queraberration nicht wiederfindet. Diese Betrachtungen gelten für eine beliebige Wellenlänge. In einem polychromatischen System werden jedoch unterschiedliche Wirkungen für die einzelnen Wellenlängen entstehen, sodaß die Queraberration für verschiedene Farben unterschiedlich ausfallen. Typischerweise werden bei visuellen optischen Systemen die Angaben für rot, grün oder blau gemacht. Die Kurven werden der einfachen Zuordnung halber in eben diesen Farben dargestellt. Diese Betrachtung ist allgemeingültig und gilt gleichermaßen für Fernrohre, Objektive oder beliebige zusammengesetzte rotationssymmetrische optische Systeme im monochromatischen Strahlengang.
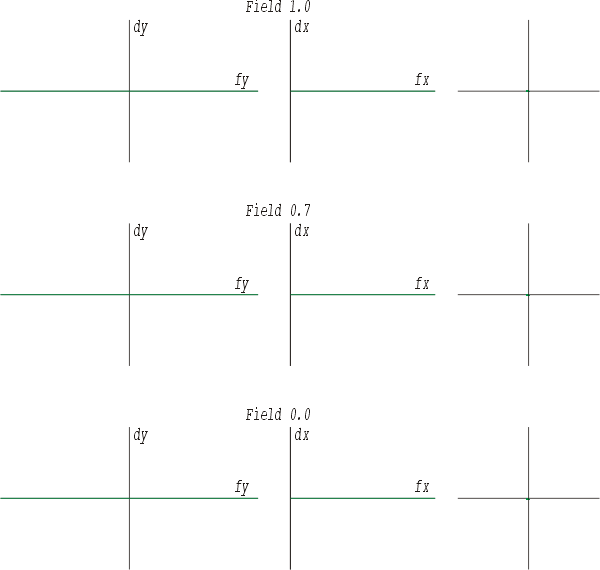
Die erste Darstellung beschreibt ein System ohne jegliche Abbildungsfehler. In den drei übereinanderliegenden Reihen sind immer zu unterst die Abbildungsleistung in der Bildmitte, ein Punkt innerhalb des Bildfeldes und oben der Bildfeldrand dargestellt. Die seitliche Ausdehnung geht einher mit der Größe des Strahlenbündels und entspricht der vollen wirksamen positiven und negativen Höhe der Eintrittspupille. Die linke Spalte zeigt die Abweichung in der meridionalen Ebene und die mittlere Darstellung die sagitale Ebene. Da die Darstellung für die sagitale Ebene auf Grund des vorher dargelegten immer symmetrisch zur Ordinate ist, wird auf die Wiedergabe der linke Seite verzichtet. Die rechte Spalte beinhaltet einen Spot.
Wie hier zu sehen, sind die Kurven in der linken und mittleren Darstellung gerade, haben keine Neigung und verlaufen exakt auf der Abszisse. Der Spot ist ein Punkt im Koordinatenursprung. Es sei angemerkt, daß es hier zunächst um rein qualitative und tendenzielle Aussagen geht und deshalb auf die Angabe eines Maßstabs verzichtet wird.

Parallel eintretende Strahlen verlassen ein auf Unendlich fokussiertes Fernrohr wieder als parallele Strahlen. Schräg eintretende Strahlen werden entsprechend der Vergrößerung abgelenkt. Das Fernrohr ergibt in dieser Konfiguration ein afokales, also brechkraftloses Instrument. Bei einem Objektiv ist das Äquivalent darin zu sehen, daß sich der Empfänger exakt in der Bildebene befindet. Wenn als einfachster Fall eine Defokussierung angenommen werden soll, sieht das Ergebnis so aus:
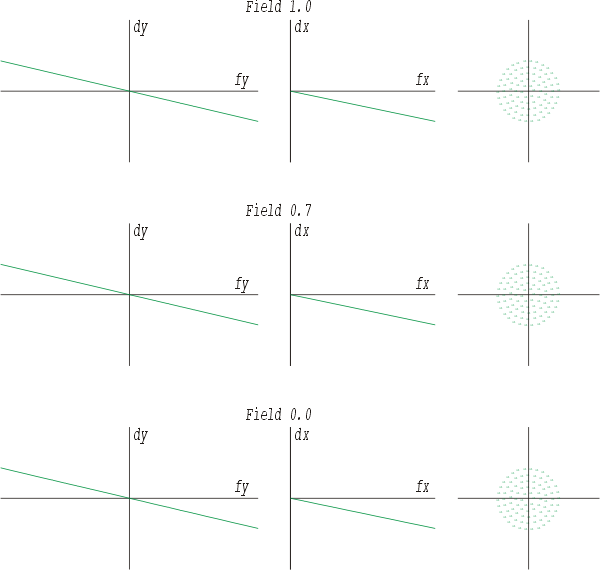
Hier wurde eine positive Veränderung vorgenommen. Also ein Objekt in Nahdistanz oder eine Verschiebung des Okulars vom Objektiv weg. Die Umkehrung erzeug folgendes charakteristische Bild:
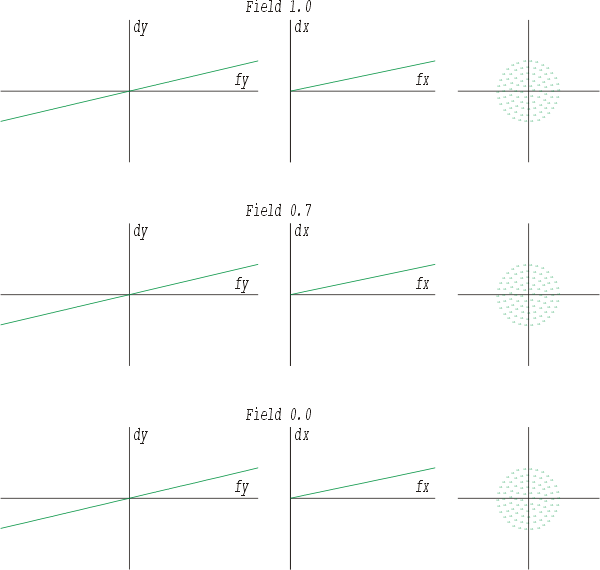
Bei der Defokussierung handelt es sich nicht wirklich um einen Bildfehler, da eine Korrektur allein durch das richtige Einstellen der Afokalität über den Abstand zwischen Objektiv und Okular bei Fernrohren oder durch die Lage der Bildebene bei Objektiven erfolgen kann, womit wieder der oben gezeigt Idealzustand erreicht wird. Die Kurven werden dabei um den Koordinatenursprung gedreht, bis sie auf der Abszisse zu liegen kommen. Der Spot läuft in einem Punkt zusammen, so wie man es beim Fokussieren an einem Stern beobachten kann.
Ein sehr ähnliches Bild ergibt sich bei der Betrachtung der Feldkrümmung oder Bildfeldwölbung. Der Rand ist wie oben geneigt, jedoch liegt die Kurve in der Bildmitte bereits exakt auf der Abszisse. Korrekturversuche würden bewirken, daß der Rand scharf, jedoch dabei die Bildmitte unscharf abgebildet würde.
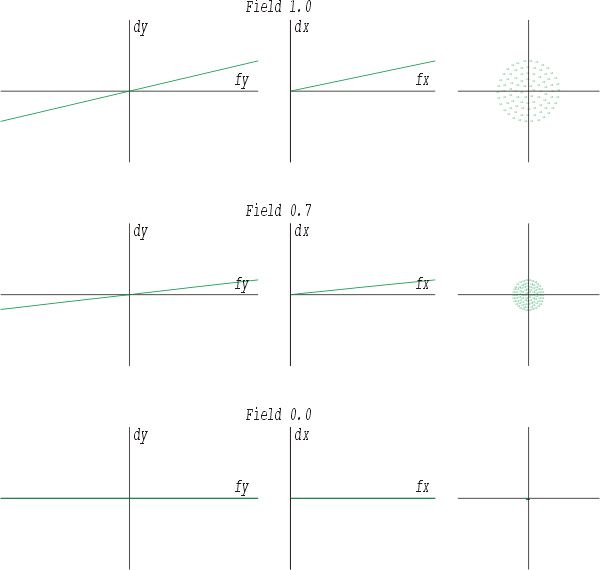
Das Ganze geht natürlich auch in negativer Richtung.
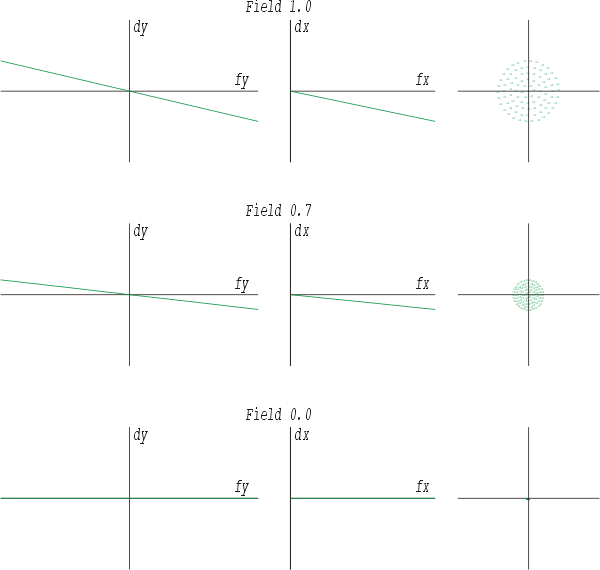
Bei dieser Betrachtungen ist es gleichgültig, ob der volle Eintrittspupillendurchmesser oder nur ein kleinerer Durchmesser angesetzt wird. Die Gerade ist nur länger, da der Wert fy die Größe der Eintrittspupille verkörpert. Mit kleinerer Eintrittspupille werden also auch die Bildfehler verkleinert. Bei der Betrachtung des nächsten Fehlers, wird das deutlich.
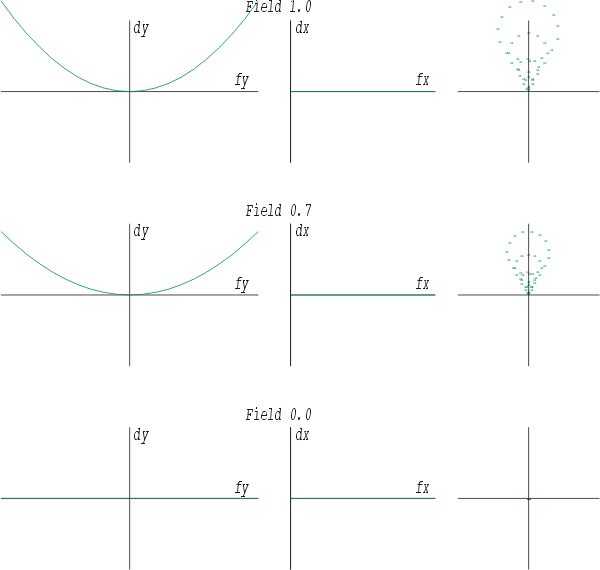
Hier ist die Koma dargestellt, die ein sehr charakteristisches Fehlerbild aufweist. Dieses entsteht, wenn ein Bündel geneigt zur Achse verläuft. Im Spotbild zeigen sich tropfen- oder kometenartige Zerstreuungfiguren mit ungleichmäßiger Lichtverteilung, die sich aus der Überlagerung verschieden großer, aber nicht konzentrischer Zerstreuungskreise ergeben und die nur zur Meridionalebene symmetrisch sind. Man spricht deshalb in diesem einfachsten Fall von meridionaler Koma.
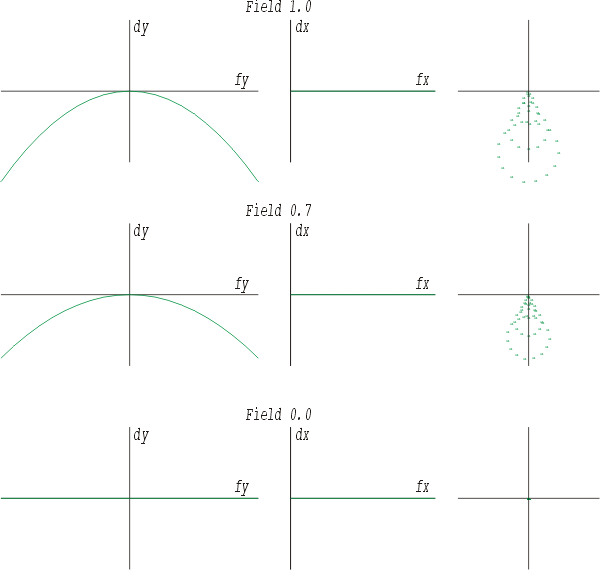
Die Koma als unsymmetrischer Öffnungsfehler kann auch mit negativem Vorzeichen behaftet sein.
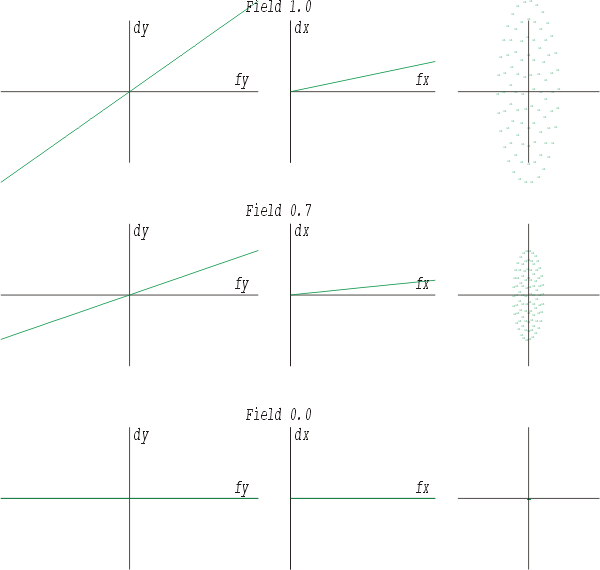
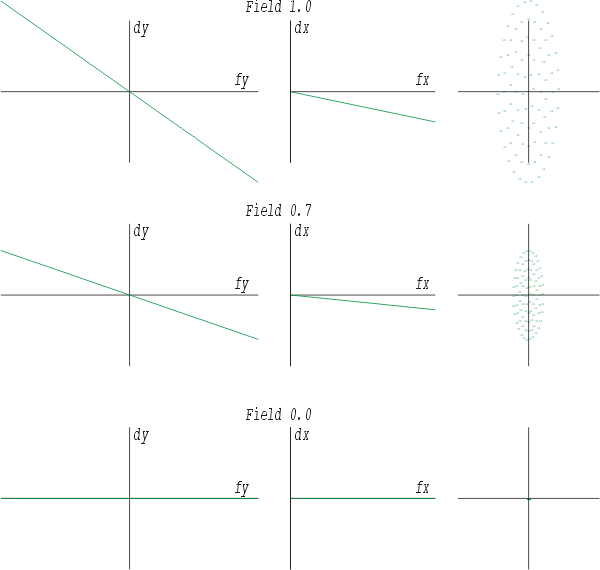
Ein weiterer Bildfehler ist der Astigmatismus, von dem hier zunächst die Variante mit positivem Vorzeichen gezeigt ist. Astigmatismus (Punktlosigkeit) betrifft auch Strahlenbündel, die schräg eintreffen. Der Querschnitt dieses Strahlenbündels ist in der Schnittebene der Linse nicht kreisrund, sondern elliptisch. Die längere (meridionale) Schnittebene unterliegt daher einer stärkeren sphärischen Aberration als die kürzere (sagittale). Damit ergeben sich für diese Strahlenbüschel unterschiedliche Brennpunkte. Ein heller Punkt am Bildrand wird daher als tangentialer (im sagittalen Brennpunkt) oder radialer Strich (im meridionalen Brennpunkt) in zwei Ebenen abgebildet. Der Fehler äussert sich in Schärfeabfall zum Bildrand hin.
Ein negativer Astigmatismus stellt sich dann so dar.
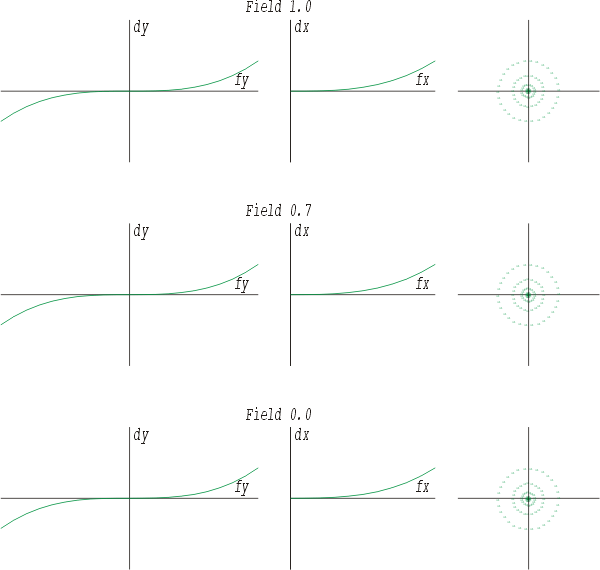
positive sphärische Aberration
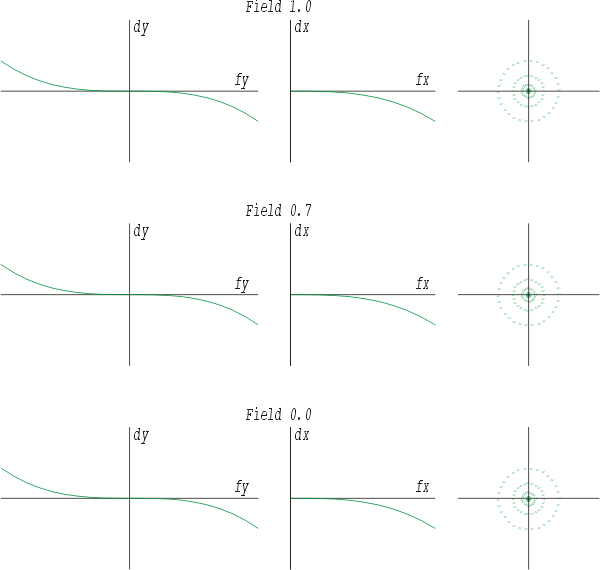
negative sphärische Aberration
Als weiterführende Literatur kann verwiesen werden auf:
| Autor | Titel | Ausgabe | Bemerkungen |
|---|---|---|---|
| Welford, W. T. | Aberrations of the Symmetrical Optical Systems | 1974, London, Academic Press | 240 Seiten |
| Welford, W. T. | Geometrical Optics Optical Instrumentation | 1962, Amsterdam, North-Holland Publishing Company | 200 Seiten, 360 Abb., Gr.8° |
| Buchdahl, H. A. | Optical Aberration Coefficients | 1954, London, Oxford University Press | XX, 336 Seiten, Gr. 8° |
| Hopkins, H. H. | Wave Theory of Aberrations | 1950, London, Oxford University Press |
169 Seiten |